|
D: 10 Jan 2026 Main functions (--make-grm-bin...) Quick index search |
Data Exploration 2 - Genomic Structure - Relationship MatrixThis is Part B of the Genomic Structure tutorial. If you have not run Linkage, then start there. You can also skip ahead by generating the files from that tutorial, Tutorial Shortcuts - Linkage. Run this in the R console to load necessary functions for the examples below. If this does not work then make sure you have gone through the Setting Up the Plink 2 Tutorial. R:source("../R/popstrat.R")
Part 3: RelationshipsWe start with examining population structure by creating the similarity matrix between individuals (aka relationship matrix), U. Plink 2 has two general methods for this. The first belongs to what is called identity-by-similarity (IBS) and is created using --make-rel (referred here and in Plink as the genomic relationship matrix, GRM). The other belongs to the class of identity-by-descent (IBD) relationship matrices. It is created using --make-king (referred here and in Plink as KING). (Plink 2 uses the KING algorithm from Manichaikul et al., 2010.) The IBS algorithm is agnostic to the genealogical roots between individuals; whereas, IBD methods infer co-segregation of genetic elements from ancestors.time plink2 \
--pfile ./data/processed/all_hg38_qcd \
--make-rel square0 \
--maf 0.1 \
--out ./results/qc/qc3/all_hg38_qcd_grm
--make-rel square0Makes the GRM relationship matrix as a square matrix with zeros for the upper triangle. --maf 0.1 Note that previously, we pruned the dataset for maf<0.05. However, Plink 2 may throw an error due to a discrepancy in allele counts in the founder vs nonfounders. Adding a more stringent threshold fixes this. Also, what allele is called minor and the allele counts change with different populations. Thus additional maf pruning may make sense when we isolate subpopulations. In addition, due to precedence across these tutorials, we used an odd double MAF filtering. (We may change this in future versions of the tutorial.) However, it may make more sense to filter MAFs at the subpopulation level due to substantial cross-population differences and then use the intersection across them to re-pool the subpopulations. Of course, you can only do this if you have some idea of the population structure. Now, make the equivalent KING matrix (about 5 minutes on 2020 M1 MBP). Plink 2: time plink2 \
--pfile ./data/processed/all_hg38_qcd \
--make-king square0 \
--maf 0.1 \
--out ./results/qc/qc3/all_hg38_qcd_king
--make-king square0Makes the KING relationship matrix as a square matrix with zeros for the upper triangle. Let's plot the distribution of calculated relationships. Note that parent-child pairs are expected to share about 50% of their genomes (for GRM this should be about 0.5, and for KING 0.25). We'll use R to generate some histograms. R: df<-merge_rel50("./results/qc/qc3/all_hg38_qcd_grm", "rel")
plot_rmathist_with_markers(df$z$Values,df$merged_df$Values,'GRM',k=1e3,poplabel = "ALL",er50=0.5,r50color="blue")
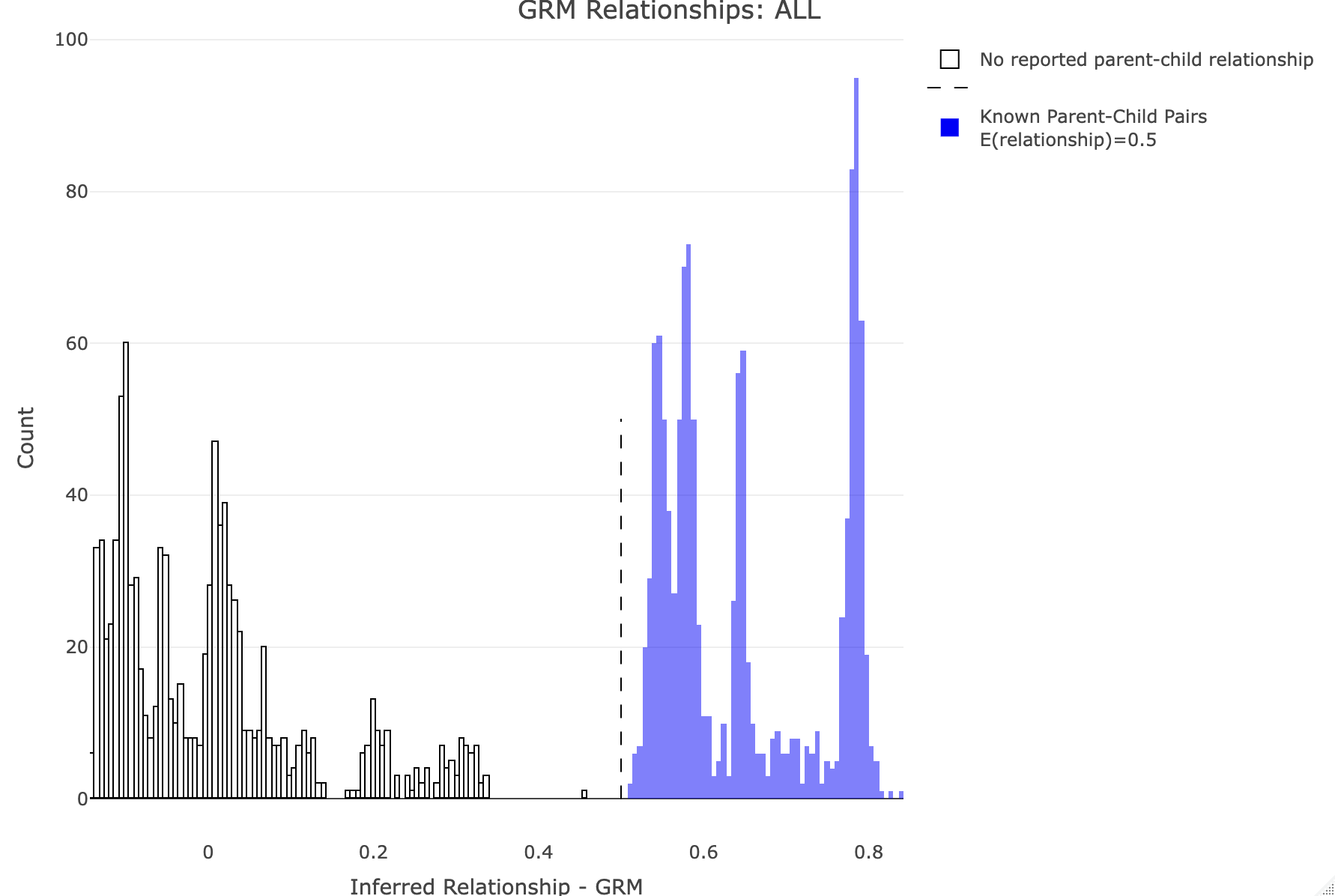
df<-merge_rel50("./results/qc/qc3/all_hg38_qcd_king", "king")
plot_rmathist_with_markers(df$z$Values,df$merged_df$Values,'KING',k=1e3,poplabel = "ALL",er50=0.25,r50color="blue")
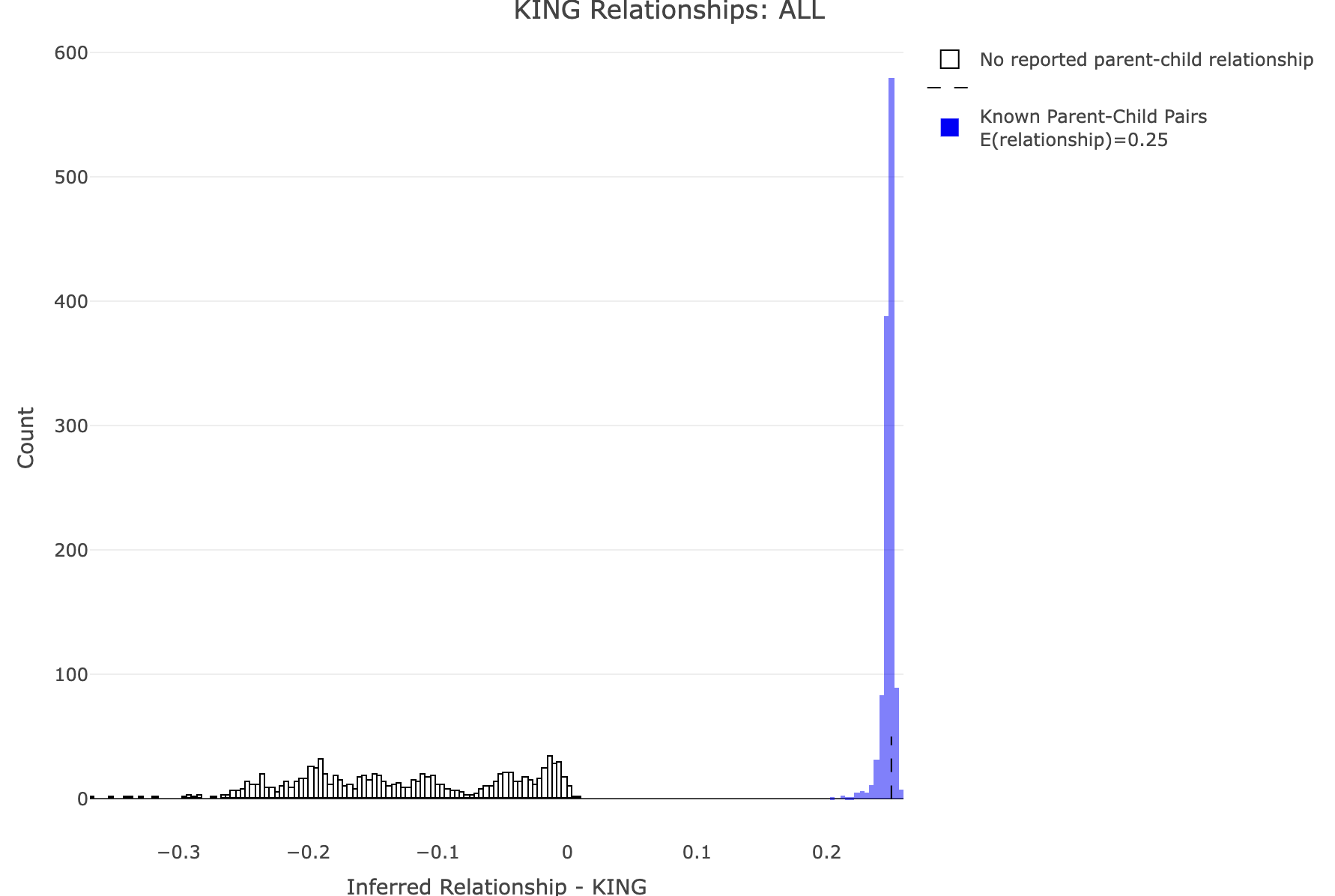
time plink2 \
--pfile ./data/processed/all_hg38_qcd \
--make-rel square0 \
--maf 0.1 \
--keep-if SuperPop==AFR \
--out ./results/qc/qc3/all_hg38_qcd_AFR_grm
--keep-if <your rule based on the phenotype data given>Removes all samples which don't satisfy a comparison predicate on a phenotype or covariate, while --remove-if does the reverse. Syntax and treatment of missing values is the same as for --extract-if-info. For binary phenotypes, either '2' or 'case' (any capitalization) can be used to refer to cases, and either '1', 'ctrl', or 'control' can be used to refer to controls. In this example, SuperPop is a column label in the all_hg38_qcd.psam file. AFR is a value in that column. SuperPop==AFR is the boolean operator indicating whom to keep. Alternatively, you can use values from a covariate file (see --covar). This command is limited to a single boolean operator. Plot GRM for AFR R: df<-merge_rel50("./results/qc/qc3/all_hg38_qcd_AFR_grm", "rel")
plot_rmathist_with_markers(df$z$Values,df$merged_df$Values,'GRM',k=1e3,poplabel = "AFR",er50=0.5,r50color="orange")
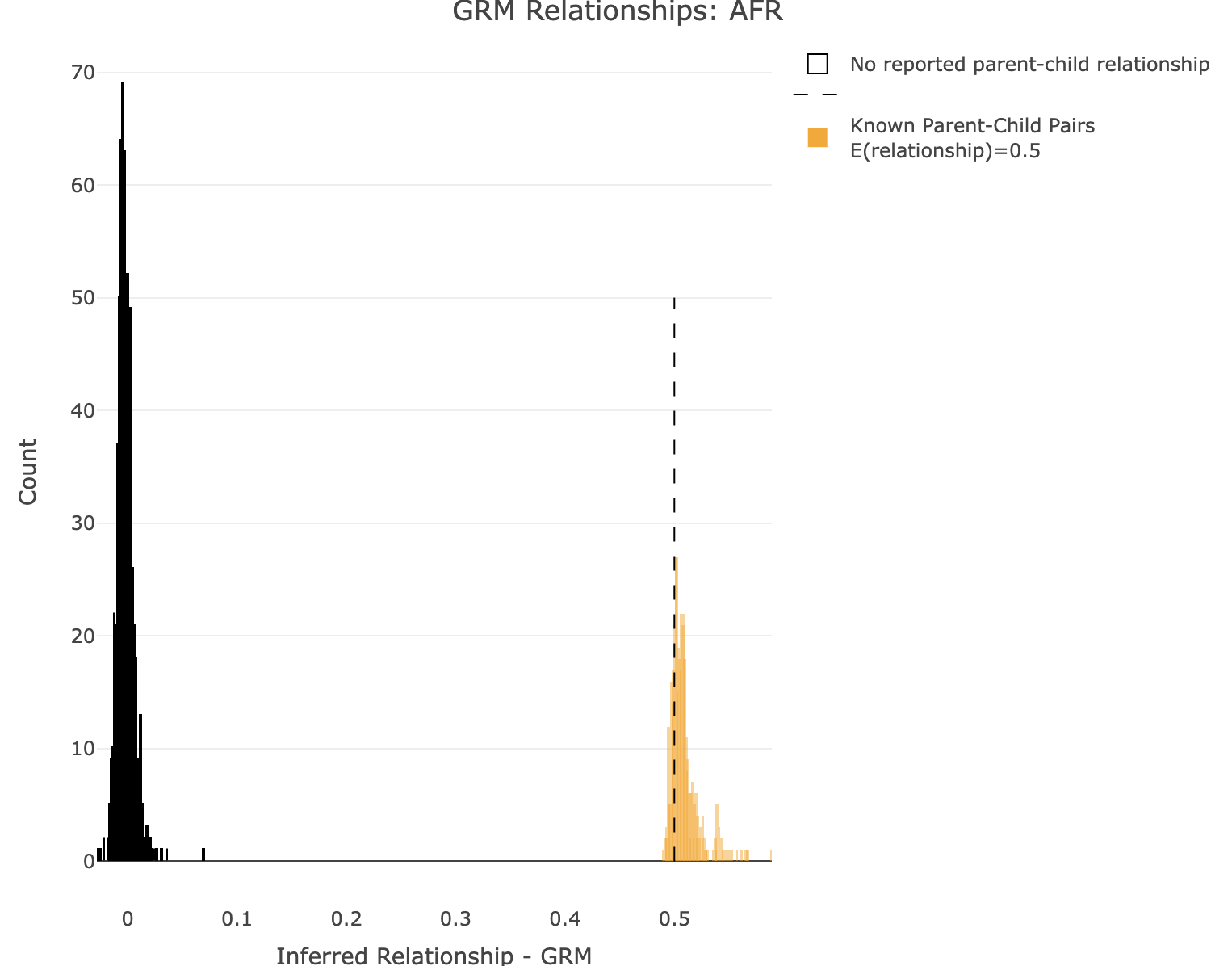
time plink2 \
--pfile ./data/processed/all_hg38_qcd \
--make-rel square0 \
--maf 0.1 \
--keep-if SuperPop==AMR \
--out ./results/qc/qc3/all_hg38_qcd_AMR_grm
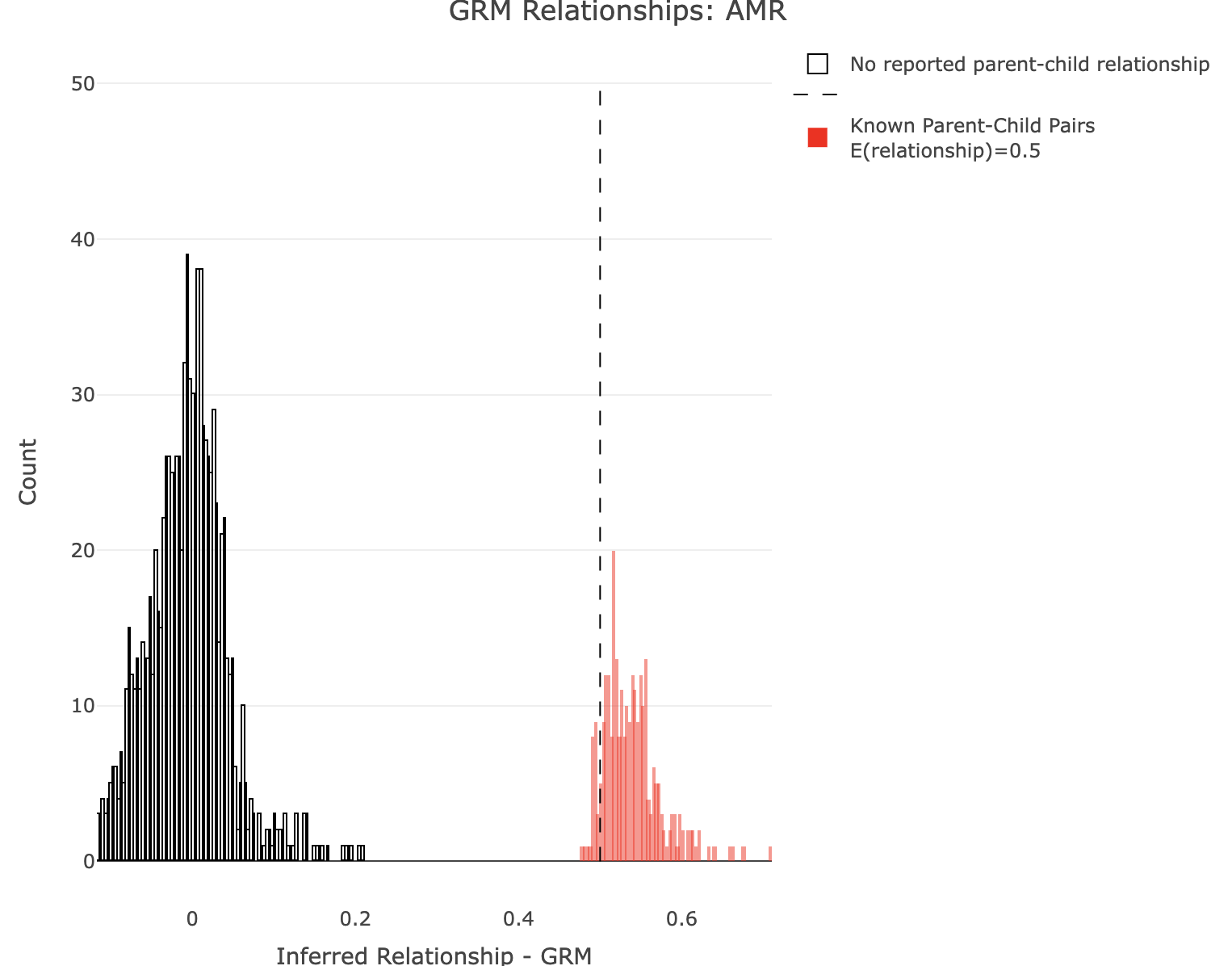
Plot GRM for AMR.
R:
df<-merge_rel50("./results/qc/qc3/all_hg38_qcd_AMR_grm", "rel")
plot_rmathist_with_markers(df$z$Values,df$merged_df$Values,'GRM',k=1e3,poplabel = "AMR",er50=0.5,r50color="red")
time plink2 \
--pfile ./data/processed/all_hg38_qcd \
--make-king square0 \
--maf 0.1 \
--keep-if SuperPop==AMR \
--out ./results/qc/qc3/all_hg38_qcd_AMR_king
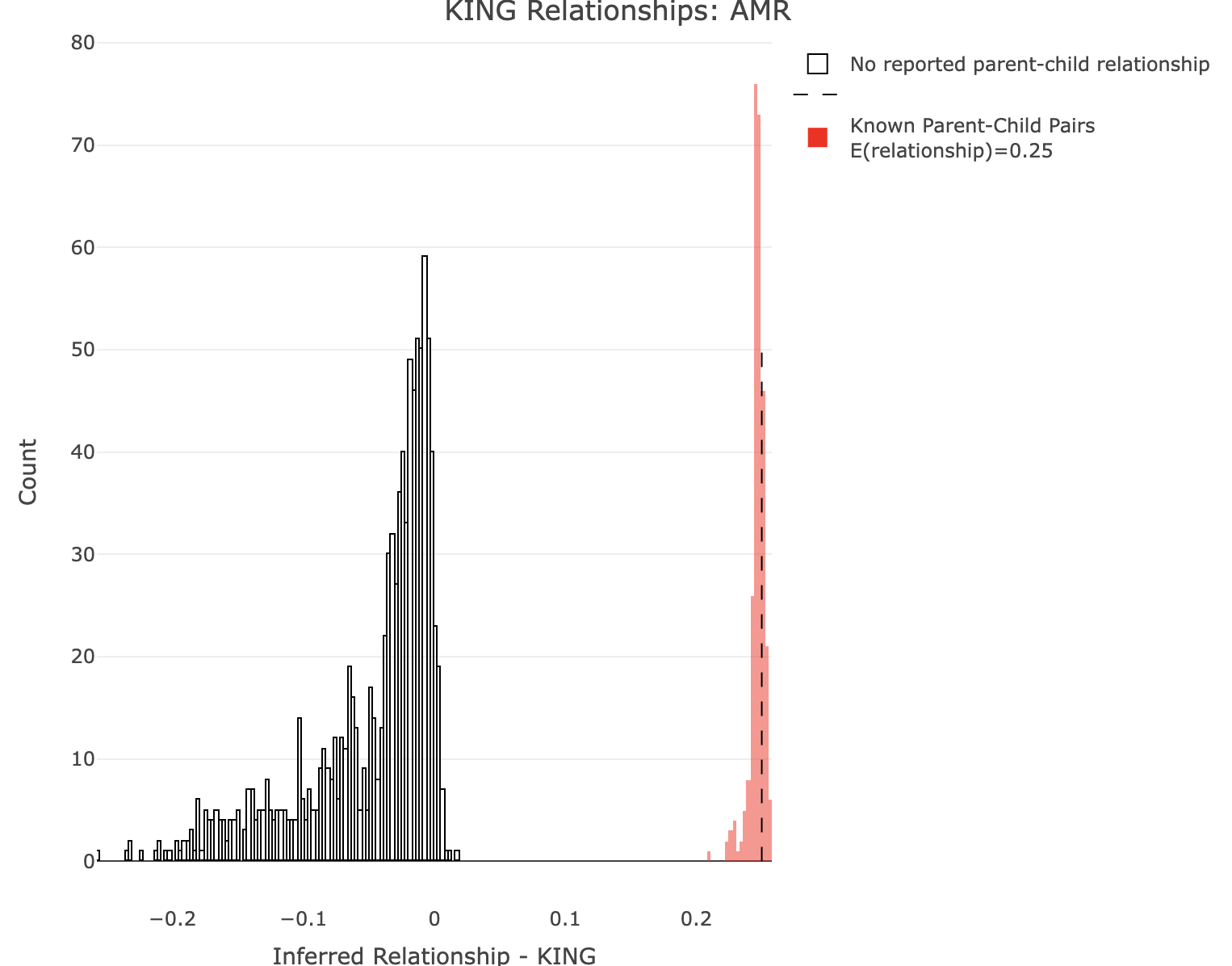
Plot KING for AMR.
R:
df<-merge_rel50("./results/qc/qc3/all_hg38_qcd_AMR_king", "king")
plot_rmathist_with_markers(df$z$Values,df$merged_df$Values,'KING',k=1e3,poplabel = "AMR",er50=0.25,r50color="red")
Part 4. Characterizing Population StructureCharacterizing population structure combines a number of the concepts in the Genomic Structure tutorial set. For this, we leverage the relationship matrix and illustrate how it relates to its dual, the LD or variant space. Population structure is often characterized by decomposing the relationship matrix into principal components or axes of variation, using Principal Components Analysis (PCA). We'll use an LD pruned version of the global population QC'd data. This was generated in the Linkage tutorial. Go back to this tutorial or Tutorial Shortcuts - Linkage, if you do not have these files. Before we begin, we will remove the 'NA' labelled individuals in 1kGP3. Create HG-only PCs. Plink 2: 1. Remove 'NA' individualstime plink2 \
--pfile ./data/processed/all_hg38_qcd_LE1 \
--make-pgen \
--remove ./misc/naiid.txt \
--out ./data/processed/all_hg38_qcd_LE1_HGonly
--remove ./misc/naiid.txtRemove all IIDs with 'NA' using the included tutorial file for these ids. 2. Compute HG-only PCs time plink2 \
--pfile ./data/processed/all_hg38_qcd_LE1_HGonly \
--freq counts \
--keep-founders \
--pca biallelic-var-wts \
--out ./results/qc/qc3/all_hg38_qcd_LE1_HGonly_pca
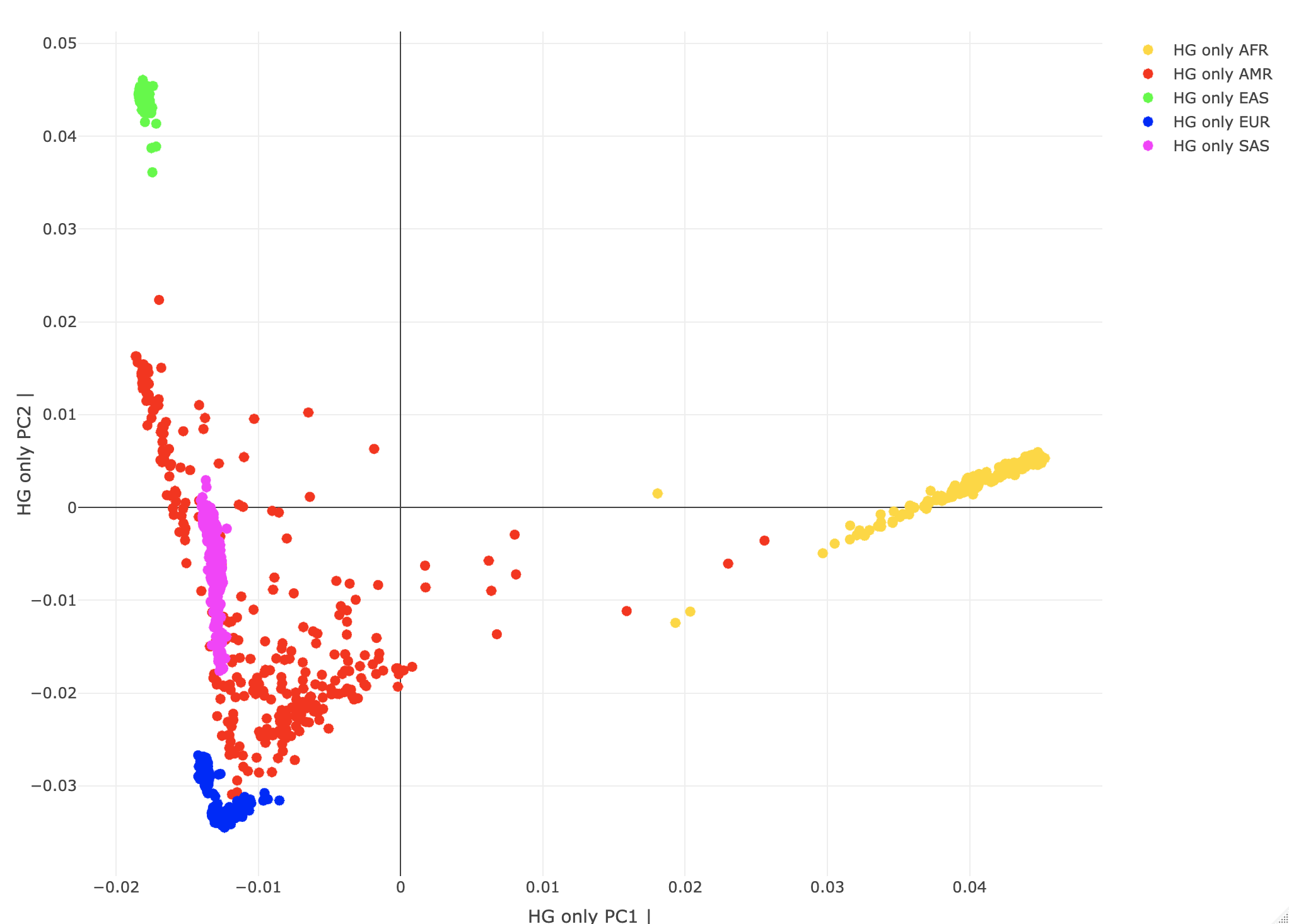
--pca biallelic-var-wtsThis runs the PCA on a GRM matrix (computed when calling PCA). The biallelic-var-wts argument saves the allele weights that we will use for projections. We'll talk about this more later. --freq counts Generates the allele frequency counts needed for the projections. Using R, let's plot the HG-only individuals by their "population" PC scores. A<-gen_popstrat_A('all_hg38_qcd_LE1_HGonly')
popstrat_plot2d(A,c("PC1","PC2"), Aprefix="HG only")
Individuals are color-coded by assigned SuperPopulation IDs. (Note Rstudio plotly is a little quirky with saving/exporting the images. You may need to try exporting it a few times to save.)
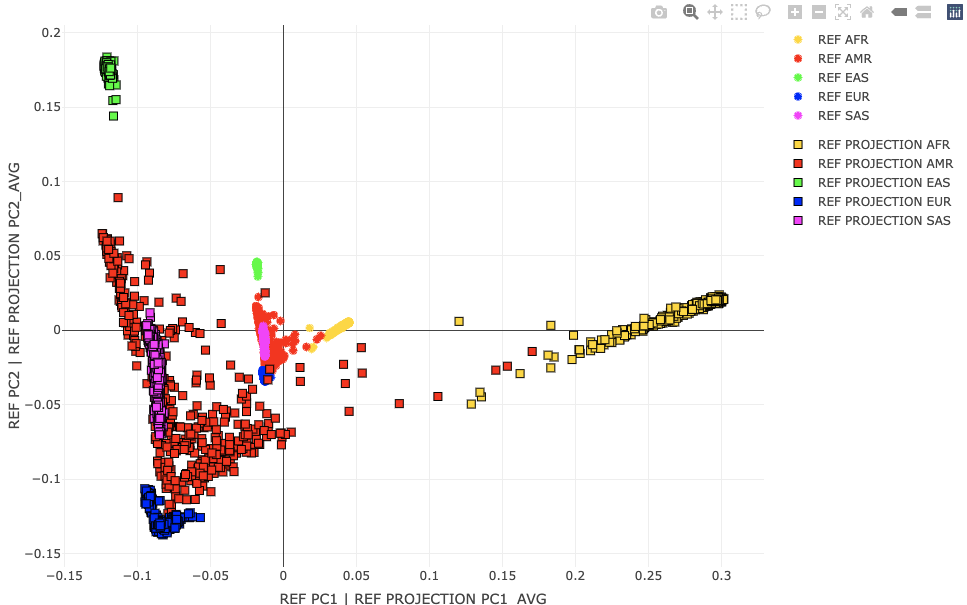
Population ProjectionsNow that we know how to make a population map, let's see how we can project new individuals into this space. That's a nicety of linear algebra. We can perform PCA on people space U and recreate the PCs in the genotype space V, through the SVD identity (underlying PCA) G=UΣVT. This saves us a lot of unnecessary computation and memory. The people PCs represent loadings across genotypes. So to get PC1 in the genotype space, we take a weighted sum across individual genotypes with weights given by their loading on the people PC1 axis. Fortunately, Plink 2 does this G,U → V mapping for us but with a warning about scaling. Let's see what the scale warning is about by projecting the HG-only data (called REF from here on) through the PCs generated using the exact same HG-only (REF) data. We may hypothesize that these should be exactly the same. Project REF against the REF-generated allele weights. Plink 2:time plink2 \
--pfile ./data/processed/all_hg38_qcd_LE1_HGonly \
--read-freq ./results/qc/qc3/all_hg38_qcd_LE1_HGonly_pca.acount \
--score ./results/qc/qc3/all_hg38_qcd_LE1_HGonly_pca.eigenvec.var 2 4 header-read no-mean-imputation variance-standardize \
--score-col-nums 5-14 \
--out ./results/projections/all_hg38_qcd_LE1_HGonly_HGonlyproj
Applies linear scoring system to each sample, and reports results to *.sscore. More precisely, if G is the full genotype/dosage matrix (rows = alleles, columns = samples) and a is a scoring-system vector with one coefficient per allele and then divides by the number of allele observations (i.e. usually twice the number of variants. The input file must have exactly one line per scored allele. Variant IDs are read from column #i and allele codes are read from column j, where i defaults to 1 and j defaults to i+1. 'header-read' causes the first line of the input file to be treated as a header line containing score names. The 'no-mean-imputation' modifier throws out missing observations (decreasing the denominator in the final average when this happens). See Linear scoring, for more details. --score-col-nums 5-14 By default, a single column of coefficients is read from column #k when using --score, where k defaults to j+1. To specify multiple columns, use --score-col-nums. --read-freq ./results/qc/qc3/all_hg38_qcd_LE1_HGonly_pca.acount Loads allele frequency estimates from a --freq (PLINK 1.x ok), --geno-counts, or PLINK 1.9 --freqx report, instead of imputing them from the immediate dataset. This can mitigate issues when a small subset of a larger dataset or population is used. Now, let's visualize the projected population coordinates for the REF set against their original population coordinates. R: A2 <- loadplink2Rmat("./results/projections/all_hg38_qcd_LE1_HGonly_HGonlyproj.sscore")
popstrat_plot2d(A,c("PC1","PC2"), Aprefix="REF", A2, c("PC1_AVG","PC2_AVG"),A2prefix="REF PROJECTION")
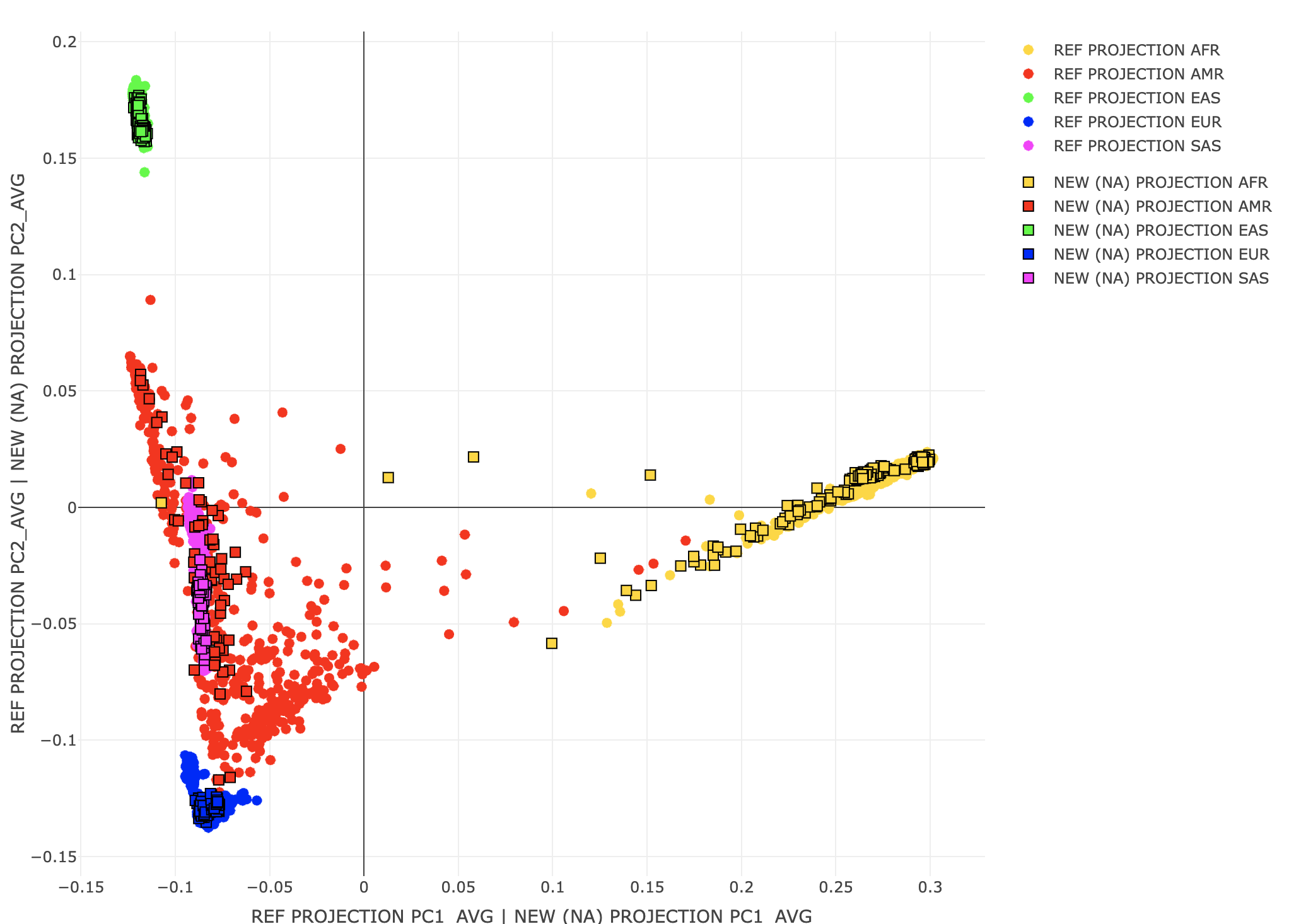
Scaling between the original REF coordinates in the sample PC space and a new sample (or original REF) projected against the variant PCs is challenging. Simply scaling by the singular values does not work. One solution (1) is to use the same projection method for the REF and new samples. However, even this will not always work. One potential issue is underestimating population structure (shrinkage) that can happen with high dimensional problems. A second issue is that these PCs may represent LD structure vs individual differences. In this case, intended population covariates may lower GWAS signal for these genetic variants. Plink 2 may include correction factors in future versions. For more details, see the Ancestry PCA references on the Rules of Thumb page. time plink2 \
--pfile ./data/processed/all_hg38_qcd_LE1 \
--keep ./misc/naiid.txt \
--read-freq ./results/qc/qc3/all_hg38_qcd_LE1_HGonly_pca.acount \
--score ./results/qc/qc3/all_hg38_qcd_LE1_HGonly_pca.eigenvec.var 2 4 header-read no-mean-imputation variance-standardize \
--score-col-nums 5-14 \
--out ./results/projections/all_hg38_qcd_LE1_HGonly_NAproj
A3<-loadplink2Rmat("./results/projections/all_hg38_qcd_LE1_HGonly_NAproj.sscore")
popstrat_plot2d(A2,c("PC1_AVG","PC2_AVG"), Aprefix="REF PROJECTION",A3,c("PC1_AVG","PC2_AVG"),A2prefix="NEW (NA) PROJECTION")
Let's generate the whole 1kGP3 PCs (HG and NA) for later tutorials. Plink 2: time plink2 \
--pfile ./data/processed/all_hg38_qcd_LE1 \
--freq counts \
--keep-founders \
--pca biallelic-var-wts \
--out ./results/qc/qc3/all_hg38_qcd_LE1_pca
|