D: 6 Dec 2024

Main functions

  (--make-grm-bin...)

Tutorials

Data Exploration 2 — Genomic Structure

Relationship Matrix

Genome-Wide Assocation Analyses (GWAS)

Post-Hoc

Formatting Files

Variant IDs

Reference Alleles

Format for R

Shortcuts

Quick index search

Data Exploration 2 - Genomic Structure - Linkage

Significance

Characterizing population genomic structure (including familial relationships) is both a compelling research objective, and can have a significant impact on GWAS (genotype-phenotype association) findings.

Studies of genomic structure can roughly be broken down into two related spaces. These are appreciated by defining a genomics matrix, G, consisting of n-samples (individuals) and p-measures (genetic variants). This defines a row (samples/individual-space) and column (genetic-variants-space). In matrix form, it can be appreciated that these spaces are intrinsically related, thus operations in one space impact the other. This is further appreciated by considering that G=UΣV.T, where U are the sample-space eigenvectors and V the variant-space eigenvectors. When G is standard-normalized these are the respective principal components (PCs) for the sample- and variant-spaces. In other words, let's say that we estimated the sample-space PCs U. These samples (individuals) coordinates can be used to visualize similarities and differences between individuals. Let's say now that we want to see where new individuals lie against these reference samples. To do this, we need V. We can either blindly run a PCA() computer command (or SVD() in many cases) as we did to get U or note that we can derive V from G, U, and Σ. V is the weighted sum of individual genotypes scaled by Σ. The take away is that principal genomic vectors are exactly determined by the individuals in your dataset and vice-versa. On one hand, this fundamental relationship complicates "ancestry" applications due to sampling biases in both the samples/individual- and variant-space. On the other hand, purposeful biased sampling methods can be leveraged to glean different insights from the same GWAS dataset. For example, Vattikuti et al., 2012 and Zaitlen et al., 2013, have taken advantage of these properties to learn different aspects of heritability by common and rare variants.

Objective

In this tutorial we will explore common Plink 2 methods used to characterize structure in the genetic variant and individual spaces.

We will use the 1000 Genomes Phase 3 data (1kGP3), see 1000 Genomes website and Nature paper. You should have this raw data in your /GWAS/project1/data/raw/ folder. If not see Setting Up the Plink 2 Tutorial. The latter also explains the expected compute environment. Do not proceed until you have read through it.

Part 1: Preprocess Data

Let's create a cleaned up dataset for the following examples. We will also recode the variant IDs to avoid duplicate ID issues. This can be an issue for these exercises. The resultant processed data ./data/processed/all_hg38_qcd.* will be our starting point for all the following analyses.

Plink 2:

time plink2 \ --pfile 'vzs' ./data/raw/all_hg38 \ --make-pgen \ --autosome \ --snps-only \ --hwe 0.05 keep-fewhet \ --maf 0.05 \ --set-all-var-ids @:#\$r,\$a \ --out ./data/processed/all_hg38_qcd

--autosomes and --snps-only
Restrict the variants to autosomal chromosomes and single nucleotide polymorphisms.

--hwe 0.05 keep-fewhet
Threshold (remove) variants with a P-value <0.05 (higher p removes more) that violate hardy-weinberg equilibrium - see Data Exploration 1 - Basic Statistics (HWE, Allele Frequency Spectrum).

keep-fewhet
Keeps variants that show excess homozygosity. These may be due to population structure rather than genotyping error.

--maf 0.05
Removes variants with minor allele frequencies less than 0.05.

--set-all-var-ids @:#\$r,\$a
Recodes the variant IDs to unique labels with @=chromosome, #=basepair position, \$r=reference allele, and \$a=alternative allele.

Usage Note: Plink 2 requires unique variant IDs for some functions. If this is not the case, it will error out and log this issue. This dataset has non-unique IDs (likely due to multiallelic variants being split into separate lines). Here we recode them as above. Another option is to remove duplicate IDs. For this use --rm-dup.

Part 2: Linkage Disequilibrium (LD)

Here we will estimate the non-random co-segregation of alleles at different loci; aka, linkage disequilibrium (LD). In other words, how often does an allele A/a at one genomic location co-segregate with an allele B/b at another location. We only address biallelic two loci, pairwise, estimates here.

About:Coefficient of Linkage Disequilibrium, D
There are several methods for estimating LD. Historically, they have their roots in what is called the coefficient of linkage disequilibrium, D. The measure D is essentially the mathematical covariance between two loci. It is calculated by the difference in their observed joint occurrence (of AB, for example) to that expected by chance. For example, the D for allele A at locus 1 and allele B at locus 2 is given by:

D_AB=Π_AB-Π_AΠ_B,
where Π:=frequency

Note the subscript AB. That is only one of several allelic combinations or haplotypes. Typically, we want a more general metric over all pairwise allele combinations. It can be shown for two biallelic loci, that only one set needs to be computed to get the magnitude of the general D, which is what we often operate on (i.e., filter on). The sign will depend on the specific allelic pair.

Let's estimate LD using Plink 2 --r[2]-[un]phased... wait! Plink 2 needs to know if we want to run "phased" or "unphased".. Looking into the reference docs, it says that we should run "phased" for D and the like. Okay, but let's dive a little deeper into what this means.

About:Phase
Phase refers to whether the alleles at the two loci originate from the same parental chromosome. Recall that the historic definition of LD involves co-segregation and not just co-occurrence. Using (inferred) phase is one major difference between LD and a method that more naively takes the inner-product of two vectors. Traditionally, LD often referred to co-inheritance which was used for tracing causal genetic factors.

Plink 2 can use phase information if it was precomputed and part of your data (e.g., pgen). Plink 2 can also estimate phase without family trios, etc. It does this via a simple statistical model based on genotypes alone, using the cubic exact equation from Gaunt, Rodriguez, Day (2007) and maximum likelihood to select between multiple solutions. You can inspect whether multiple solutions exist and other information using Plink 2's --ld method.

Back to our exercise. Let's estimate D for 1kGP3.

Plink 2:

time plink2 \ --pfile ./data/processed/all_hg38_qcd \ --chr 22 \ --thin-count 1000 \ --seed 111 --threads 1 --memory 8000 require \ --r-phased cols=+d \ --ld-window-r2 0 \ --out ./results/qc/qc2/all_hg38_qcd_prephased_phasedr

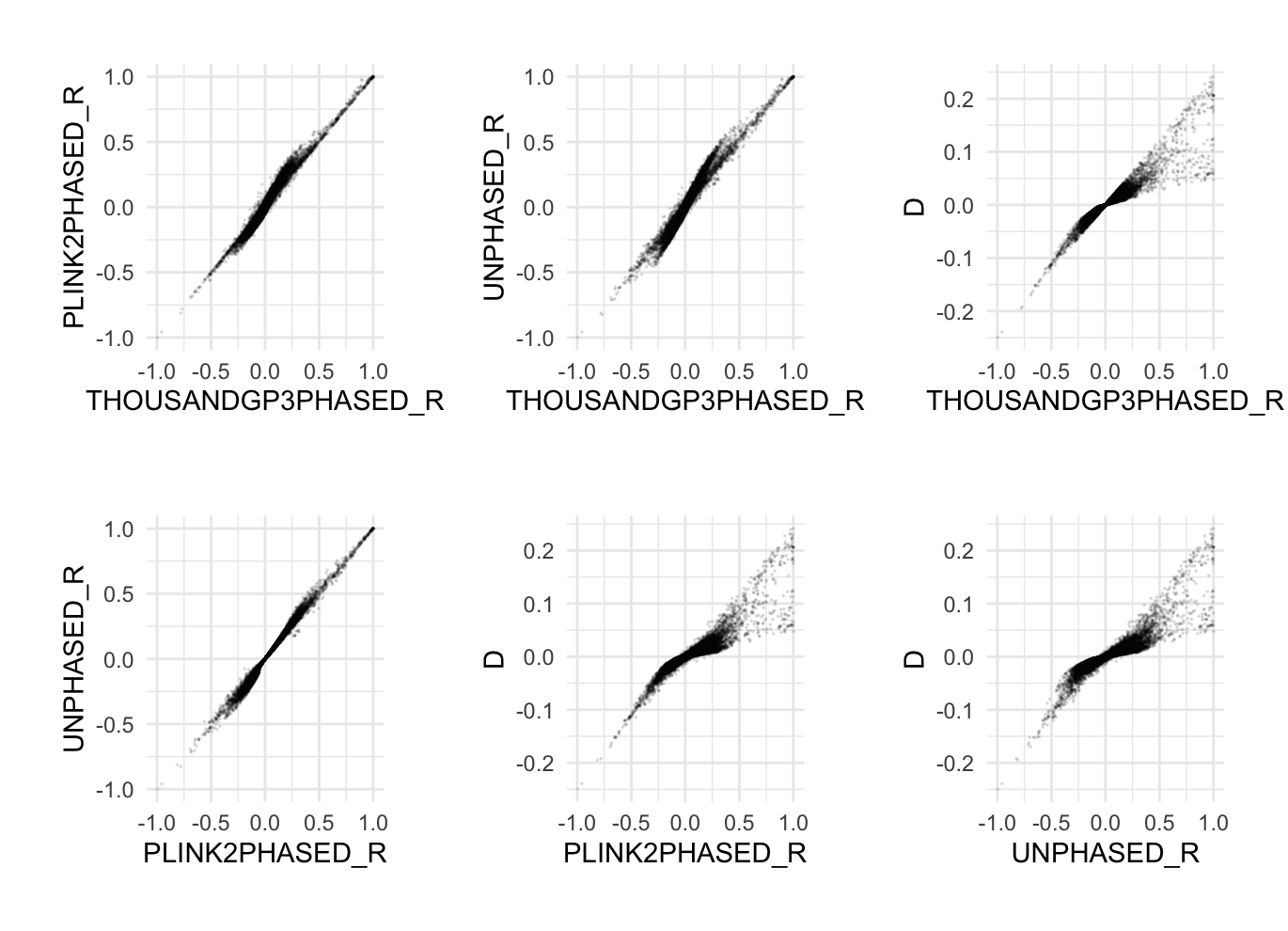
--chr 22
Restricts the analysis to chromosome 22 variants.

--thin-count
Randomly selects 1000 variants.

--seed 111 --threads 1 --memory 8000 require
Sets the random seed for replicating results.

--r-phased cols=+d
Calculates the phased r and D statistics.

--ld-window-r2 0
This removes LD filtering except for NaN. We do this for our comparisons below.

--out ./results/qc/qc2/all_hg38_qcd_prephased
Add the descriptor 'prephased' to note that the originating 1kGP3 data has precomputed phase information.

To check if your data has phase information use:
--pgen-info

About: r and different D statistics
Thus far, we only talked about D. The metric r is a correlation, aka normalized transformation of the D (covariance) value. It is given by:

r=D/(Π_A(1-Π_A)Π_B(1-Π_B))^0.5

This brings up an important aspect of using the D statistic. Although it gives information about the magnitude of associations between loci, it is a function of their allele frequencies and thus difficult to interpret across pairwise associations.

Thus it is common to rescale by some function of the allele frequencies. The statistic r uses the geometric mean of the loci variances (thus r is a correlation statistic). Another popular normalization is called D-prime that uses something like the correlation normalization (it can be called in Plink 2 using --r-phased cols=+d,+dprime). The statistics r, D, and D-prime are related but can give quite different values. In addition, the unphased r can also be different from the phased r statistic due to how the haplotype frequencies are estimated.

Let's calculate and compare four common LD statistics: 1) D using 1kGP3 prephasing, 2) phased-r using 1kGP3 prephasing, 3) phased-r using Plink 2 phasing, and 4) unphased-r. We already calculated (1) and (2) above.

Phased-r using Plink 2

1. Remove phase information from 1kGP3

Plink 2:

time plink2 \ --pfile ./data/processed/all_hg38_qcd \ --make-pgen erase-phase \ --out ./data/processed/all_hg38_qcd_unphased

--make-pgen erase-phase
Makes a pgen set of files with phase information removed.

2. Calculate phased-r using Plink 2

Plink 2:

time plink2 \ --pfile ./data/processed/all_hg38_qcd_unphased \ --chr 22 \ --thin-count 1000 \ --seed 111 --threads 1 --memory 8000 require \ --r-phased \ --ld-window-r2 0 \ --out ./results/qc/qc2/all_hg38_qcd_unphased_phasedr

Unphased-r

Plink 2:

time plink2 \ --pfile ./data/processed/all_hg38_qcd_unphased \ --chr 22 \ --thin-count 1000 \ --seed 111 --threads 1 --memory 8000 require \ --r-unphased \ --ld-window-r2 0 \ --out ./results/qc/qc2/all_hg38_qcd_prephased_unphasedr --r-unphased
Use the -unphased flag here to ignore phase information and estimate r.

Inspect Results

Now in the R console, run ...

R:

source("../R/plotLD.R")

As expected there is generally good agreement between the r statistics compared to D. While the unphased-r deviates to some degree with the phased-r using 1kGP3-phasing, this is somewhat corrected by Plink 2's inferred phase.

We'll end this tutorial with another common operation, LD pruning. LD pruning primarily reduces computational burden and mitigates bias in our analyses. However, it is important to note that removing correlated variants does not save from the posthoc analyses of determining what is the causal loci (signal) among these correlated sets. We will revisit this concept and Plink 2's --clump operation in tutorials where we perform genotype-phenotype association analyses. For now, let's create an LD-pruned dataset that we will use for other tutorials.

time plink2 \ --pfile ./data/processed/all_hg38_qcd \ --indep-pairphase 100 0.8 \ --out ./results/qc/qc3/all_hg38_qcd

time plink2 \ --pfile ./data/processed/all_hg38_qcd \ --make-pgen \ --extract ./results/qc/qc3/all_hg38_qcd.prune.in \ --out ./data/processed/all_hg38_qcd_LE1

Data Exploration 2 — Genomic Structure — Relationship Matrix >>